|
|
# 无人机飞控算法-姿态估计 此系列记录了我理解的卡尔曼滤波从0到1的过程,从姿态估计到位置估计,我们从核心点一个个出发,并结合实际模块的应用来一一揭开卡尔曼滤波的神秘面纱。
<hr/>
提示:在系列文章中,我参考了大量CSDN,知乎,简书等其他朋友的各种文档资料,并从中获益良多,对此表示非常感谢!在更新的过程中不免出现很多错误,希望大家能够及时指出和交流,一起学习,一起进步!
@TOC
<hr/>前言
作为一个非控制类出生的通信工程师,半路出家,还是挺困难的,需要学习的知识很多,主要是卡尔曼滤波方面的,包含微积分、线性代数、概率统计论、信号与系统、控制论等等。在无人机里飞控是其中重要的组成部分之一,而飞控的核心就是算法,主要包括姿态估计算法,导航控制算法,PID控制算法,路径规划算法等。此系列从姿态估计算法入手,通过IMU的姿态解算来学习姿态估计算法究竟是为何物。
<hr/>推荐:学习基础知识我推荐一下3blue1brown,在B站上可以搜索到他们的课程,讲的很生动,可以帮您快速理解一些核心知识。
一、姿态估计是什么?
想象一下,你拿着一根平衡杆,走在独木桥上,你该如何操控你手里的平衡杆才能使你不掉下去呢?从主观意识着想,其实挺简单的,如果身子往左倾斜,我们就把杆子向右移,如果身子往右倾斜,我们就把杆子向左移。要实现这个目的,首先我们是不是要知道身体现在究竟是左倾斜还是右倾斜呢?这就是姿态估计(Attitude Estimator)。那如何检测姿态呢?这就需要传感器了,在人类的身上,大脑充当了这个角色,在机器上,我们通过惯性测量单元(IMU)来测量姿态。
二、惯性测量单元(IMU)
1.陀螺仪
陀螺仪是利用高速回转体的动量矩敏感壳体相对惯性空间绕正交于自转轴的一个或二个轴的角运动检测装置。利用其他原理制成的角运动检测装置起同样功能的也称陀螺仪。陀螺仪可感测一轴或多轴的旋转角速度,可精准感测自由空间中的复杂移动动作,因此,陀螺仪成为追踪物体移动方位与旋转动作的必要运动传感器。不像加速器与电子罗盘,陀螺仪不须借助任何如重力或磁场等的外在力量,能够自主性的发挥其功能。所以,从理论上讲只用陀螺仪是可以完成姿态导航的任务的。陀螺仪的特性就是高频特性好,可以测量高速的旋转运动。缺点是存在零点漂移,容易受温度/加速度等的影响。
2.加速度计
加速器可用来感测线性加速度与倾斜角度,单一或多轴加速器可感应结合线性与重力加速度的幅度与方向。含加速器的产品,可提供有限的运动感测功能。加速度计的低频特性好,可以测量低速的静态加速度。在我们的飞行器上,就是对重力加速度g(也就是前面说的静态加速度)的测量和分析,其它瞬间加速度可以忽略。记住这一点对姿态解算融合理解非常重要。当我们把加速度计拿在手上随意转动时,我们看的是重力加速度在三个轴上的分量值。加速度计在自由落体时,其输出为0。为什么会这样呢?这里涉及到加速度计的设计原理:加速度计测量加速度是通过比力来测量,而不是通过加速度。
3.磁力计
电子罗盘也叫数字指南针,磁力计,是利用地磁场来定北极的一种方法。现在一般有用磁阻传感器和磁通门加工而成的电子罗盘。电子罗盘可由地球的磁场来感测方向。运用电子罗盘的消费性电子产品应用,包含在手机的地图应用程序显示正确方向,或为导航应用程序提供前进方向数据。然而,电子设备或建筑材料的磁场干扰,比地球磁场来得强,导致电子罗盘传感器的输出值,较容易受到各种环境因素的影响,尤其在室内更是如此,因此,电子罗盘须要透过频繁的校正,才能维持前进方向数据的准确度。
<hr/>在捷联式惯导中,一般集成6轴陀螺仪和加速度计,有一些也集成了磁力计,但是一般情况下,我们都使用外部磁力计,因为磁力计在内部很容易受到电磁干扰。
三、欧拉角
1.坐标系
在描述姿态角度的时候一定要确定好坐标系,旋转轴,旋转顺序,旋转方向,如果不确定好这些,那最后得到的旋转矩阵一定是千姿百态,保证你看的眼花缭乱,不明所以,一会又对了,一会儿又错了。关于坐标系的概念和分类大家可以去看相关文档,这里我们只讲和飞控相关的坐标系.
参考坐标系(导航系)
在飞控里常用的导航坐标系有两种:东北天和北东地。
东北天
东北天用ENU表示XYZ轴
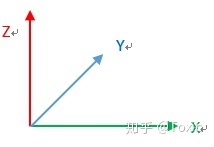
北东地
北东地用NED表示XYZ轴
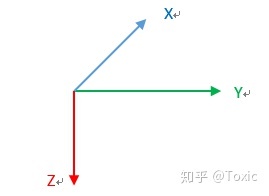
载体坐标系(机体系)
在飞控里常用的载体坐标系也有两种:右前上和前右下。
右前上
右前上表示载体坐标系的XYZ轴
前右下
前右下表示载体坐标系的XYZ轴
对应关系
ENU对应右前上

NED对应前右下

一般在惯导里用ENU较多,在控制领域里用的NED较多,飞控里也用的NED坐标系。
2.欧拉角和姿态角
欧拉角是描述旋转的一种方式,那姿态角呢?姿态角属于欧拉角的一种特殊形式,我们一般定义姿态角为偏航(Yaw),俯仰(Pitch),横滚(Roll)。在不同的载体坐标系里,姿态角对应也不一样。
ENU-右前上
右前上坐标系下,Z对应偏航,Y对应横滚,X对应俯仰。所以在常用的姿态旋转顺序(Yaw-Pitch-Roll)中,对应的旋转方式为(Z-X-Y)。
NED-前右下
前右下坐标系下,Z对应偏航,Y对应俯仰,X对应横滚。所以在常用的姿态旋转顺序(Yaw-Pitch-Roll)中,对应的旋转方式为(Z-Y-X)。前右下的旋转如下图:
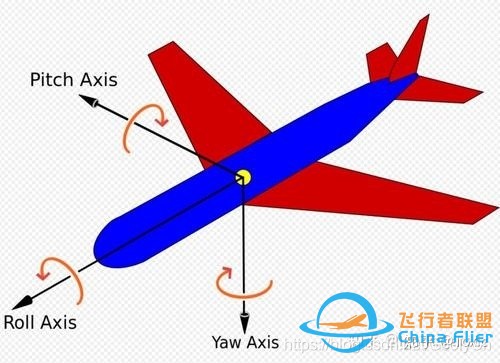
注意这里的姿态角方向都遵循右手定则。
3.旋转规则
旋转规则分两种:
- Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y) 经典欧拉角
- Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z) 卡尔丹角
每种规则都使用了3个变量描述三次旋转过程中的旋转角度, 差别在于Proper Euler angles只涉及两个转轴.而Tait–Bryan angles涉及三个转轴。 一般我们习惯使用卡尔丹角来旋转,在姿态的旋转中,一般使用(Yaw-Pitch-Roll)的旋转顺序。
旋转轴
旋转轴分绕固定坐标系旋转和绕动坐标系旋转,前者称为外旋,后者称为内旋。 - Fixed Angles 外旋 - Euler Angles 内旋
外旋(Fixed Angles)
外旋为绕静止坐标系旋转,也就是每次旋转都绕参考的静止坐标系进行三轴旋转。外旋为旋转矩阵按照先后依次左乘。
内旋(Euler Angles)
外旋为动坐标系旋转,也就是每次旋转后绕变化后的坐标系进行三轴旋转。内旋为旋转矩阵按照先后依次右乘。
在外旋和内旋中有一个特性很重要,这里先提一下:X-Y-Z的外旋等价于Z-Y-X内旋
4.万向节(Gimbal)
在欧拉角表示姿态的过程中会出现一个问题,这个问题叫万向锁。
什么是万向锁
在网上找了很多,都说的迷迷糊糊的,这里做个最通俗易懂的解释。万向锁存在于特定的旋转顺序中,当第二次进行Y轴旋转90度时就会出现万向锁,就会丢失一个方向的自由度,不太好理解吧?拿一个飞控举例,长边为Y轴,短边为X轴,垂直向下为Z轴。 飞控先平放在桌面上:

我们先进行Z轴旋转45度:

我们再绕Y轴旋转90度:

我们再绕X轴旋转45度:

注意:此刻你要从世界坐标系下观察,最开始飞控机载坐标系和世界坐标系重合,我们绕Z轴旋转了一次,也就是在水平方向上有了旋转,然后我们绕Y轴旋转90度,也就是我们在Y方向上有了旋转,现在还剩最后一个旋转X,如果我们此刻绕X轴旋转,会发生什么?在机体坐标系下,你会认为我们还是转了啊?但是在世界坐标系下,无论你在X轴怎么转,你所反应出来的效果和最开始第一次在Z轴下的旋转不是一个效果吗?飞控始终在桌面上水平旋转,只是翻了个身而已,始终无法立起来。这样的旋转虽然我是旋转了三次,但是实际上只需要旋转2次就可以达到同样的效果了,所以就没有办法表示第三个维度的旋转。反过来,从姿态A到姿态B,可以通过几种不同的方式旋转得到同样的结果,那么我们的旋转的角度就不唯一,这就是奇异点。 当然,你可以说我可以不这么转啊?我不转90度就好了吗?当然这是不可能的,旋转都是不可预测的,他可能是任意角度。 如果这里你还是不懂的话,我们在下一章旋转矩阵里再来解释这个问题!
四、旋转矩阵(DCM)
旋转矩阵又称为方向余弦矩阵,前面我们通过欧拉角来表示姿态的旋转,其实我们可以用旋转矩阵来表示旋转。本身矩阵就是为了表示旋转而生的,三个轴的旋转也就是将三个旋转矩阵相乘即可。
前提
描述旋转矩阵之前一定切记,一定要先定义好坐标系和旋转规则,否则就会把小白带入大坑深深不能自拔,本章的DCM遵循如下定义:
- 参考系:ENU或END
- 载体系:右前上或前右下
- 旋转顺序:(Yaw-Pitch-Roll)Z-X-Y或Z-Y-X
- 旋转轴:内旋
- 旋转方向:右手定则
以后在默认情况下,我们一般都遵循内旋和右手定则,只是坐标系和旋转顺序会有一些变化。
DCM推导
网上有很多DCM的推导文档,很多都没有注明坐标系和内旋外旋,导致推出来的看不懂。 我推荐一个视频大家可以看看:B站老师讲旋转矩阵
推导思路
根据我们之前提到的一个外旋内旋特性:X-Y-Z的外旋矩阵等价于Z-Y-X的内旋矩阵。 如果我们要推导内旋矩阵,那么推导出外旋的逆方向矩阵就可以了,注意这里的逆方向可不是矩阵转置。你不信可以用Matlab实验一下。为什么要先推外旋呢?因为外旋比较好理解,很直观就可以把三轴的旋转矩阵算出来。
再谈坐标系
在推导外旋旋转矩阵时,我们再分析一下坐标系,也就是ENU和NED,我们用图来对比一下两者有何区别:
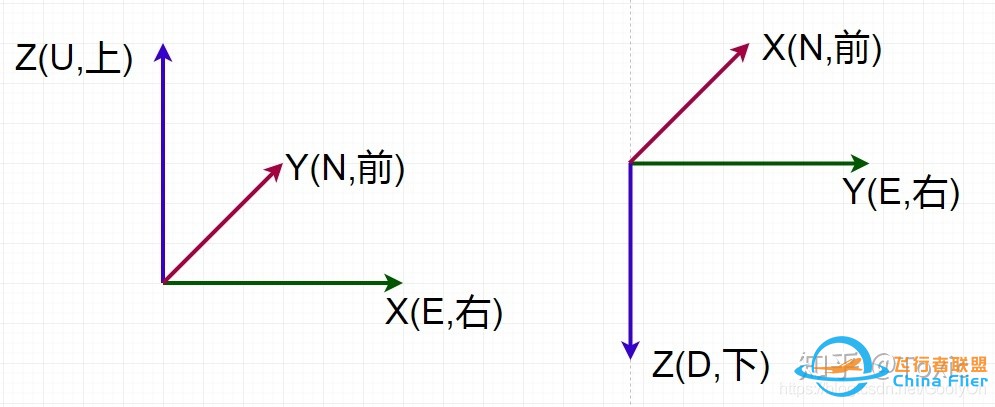
他们虽然定义的方向不一样,但同在右手定则下旋转的话,对应的顺序其实是一样的! 在ENU下,绕Z轴旋转,这时候应该是如下图所示:
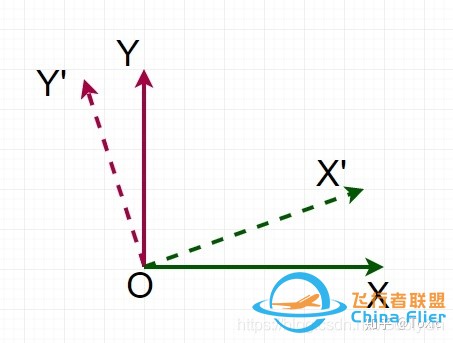
Z轴朝上,右手定则,绕Z轴转,我们只关注XY平面上发生的变化,整体变化是从XY坐标系变到了X&#39;Y&#39;坐标系,我们简称为XY变化。 在NED下,绕Z轴旋转,这时候应该是如下图所示:
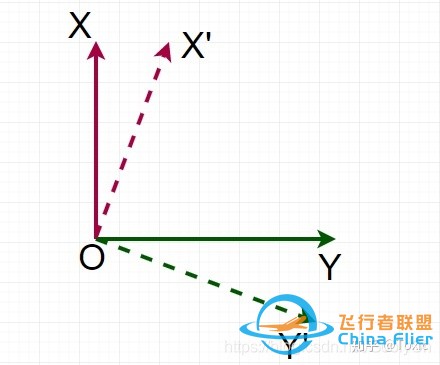
Z轴朝下,右手定则,绕Z轴转,我们只关注XY平面上发生的变化,整体变化是从XY坐标系变到了X&#39;Y&#39;坐标系,同样是XY变化。
比较两者,其实是一样的都是XY变化,同理,其他两轴也是如此!
从这里我们得到一个结论:不管是东北天还是北东地,他们所对应的单轴的旋转矩阵都是一样的,不同的无非就是旋转顺序和坐标系的定义区别而已。也就是ENU的X-Y-Z和NED的X-Y-Z是一样的,其他旋转顺序也是如此,既然外旋一样,那不同坐标系得到的最终内旋矩阵也是一样!
一般在ENU下我们用Z-X-Y,在NED下我们Z-Y-X旋转。 三轴基本旋转矩阵(外旋) 注意这里的三轴是外旋的,而且前面说了,这里不区分坐标系。
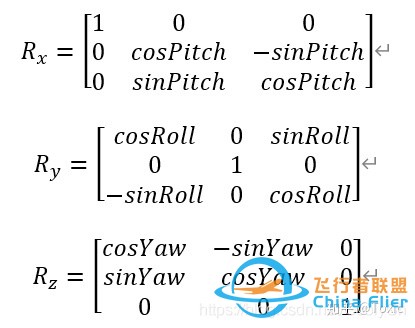
虽然旋转矩阵一样,但是我们最好还是注明坐标系,因为后面的一些运算就和坐标系有关系了。接下来我们就列举常用的几种旋转矩阵来说明。
默认情况下的旋转,参考系为n系,载体系为b系,旋转的时候,参考系不动,载体系进行旋转
ENU_Z-X-Y_Euler_Angles
- 参考系(导航系):(ENU)东北天
- 载体系(机体系):(XYZ)右前上
- 旋转顺序:Z-X-Y
- 姿态顺序:(Yaw-Pitch-Roll)偏航-俯仰-横滚
- 旋转轴:内旋
要计算内旋的Z-X-Y,我们只需要计算外旋的Y-X-Z即可,也就是计算出ENU_Y-X-Z_Fixed_Angles:

但是内旋的右乘就是从左到右乘了,从这里也可以看出左乘的Y-X-Z等于右乘的Z-X-Y了。
下面的旋转矩阵是从载体系到参考系的旋转矩阵R_b2n,左上角标有F表示是外旋下的DCM:
注意:内旋是按照旋转顺序右乘,外旋是按照旋转顺序左乘,所以内旋的Z-X-Y等于外旋的Y-X-Z。

根据外旋内旋规则那么得到内旋的旋转矩阵R_b2n:从载体系到参考系:
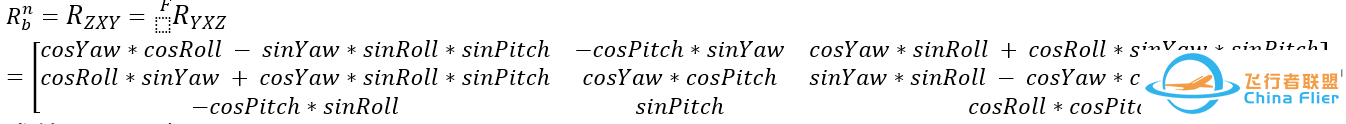
求转置可得到从参考系到载体系的旋转矩阵:
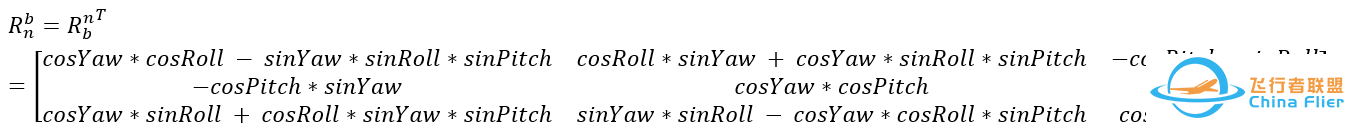
同理我们再给出其他旋转方式的DCM,过程我就不写了,直接给出结果!
ENU_Z-Y-X_Euler_Angles
- 参考系(导航系):(ENU)东北天
- 载体系(机体系):(XYZ)右前上
- 旋转顺序:Z-Y-X
- 姿态顺序:(Yaw-Pitch-Roll)偏航-俯仰-横滚
- 旋转轴:内旋 此刻我们变成了Z-Y-X旋转,注意此刻我们的姿态旋转顺序变成了(Yaw-Pitch-Roll,Z-Y-X): 注意这里的Y轴变成了Pitch,这似乎不合之前坐标系的对应关系。这无大碍,看你最后选的坐标系定了,你也可以把Y轴定义为Roll,但是在东北天下,显得怪怪的,萝卜白菜,各有所爱嘛。
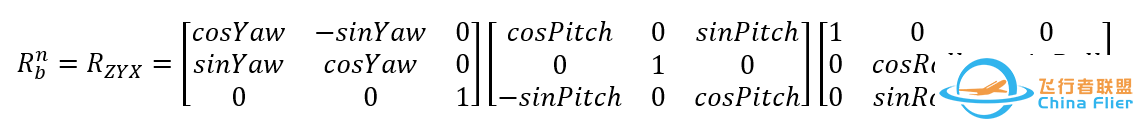
这个旋转矩阵是从载体系到参考系:
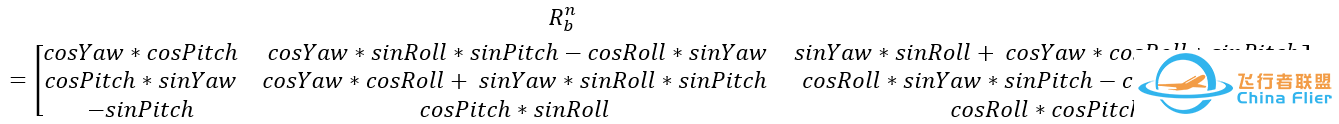
求转置可得到从参考系到载体系的旋转矩阵:
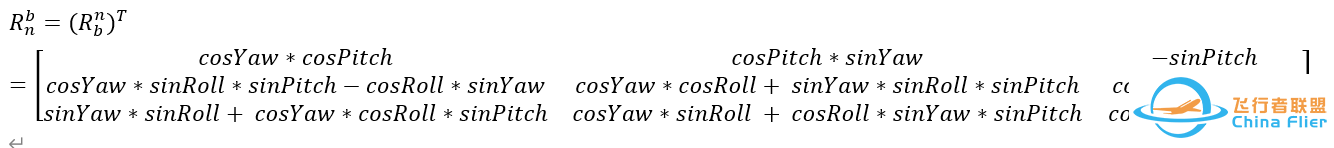
NED_Z-Y-X_Euler_Angles
- 参考系(导航系):(NED)北东地
- 载体系(机体系):(XYZ)前右下
- 旋转顺序:Z-Y-X
- 姿态顺序:(Yaw-Pitch-Roll)偏航-俯仰-横滚
- 旋转轴:内旋 前面我们说了,旋转矩阵和坐标系无关,所以NED下的ZYX和ENU下的ZYX是一样的哦,唯一不同的就是,姿态的命名和正负方向不一样了,绕X轴变成了横滚,绕Y轴变成了俯仰,Z轴还是偏航。
这个旋转矩阵是从载体系到参考系:
求转置可得到从参考系到载体系的旋转矩阵:
我们主要列出了3个DCM包括ENU下的2种和NED下的1种,这三种是比较常用的,其余的大家有兴趣可以自行推导!
再谈万向锁
如果在上一章中,你没有完全弄懂为什么欧拉角会有万向锁的问题,这里我们通过DCM矩阵来分析一下,我们用NED下的Z-Y-X旋转DCM矩阵来分析:
如果我们在Pitch方向上旋转90度,cosPitch=0,sinPitch=1,化简矩阵得到:
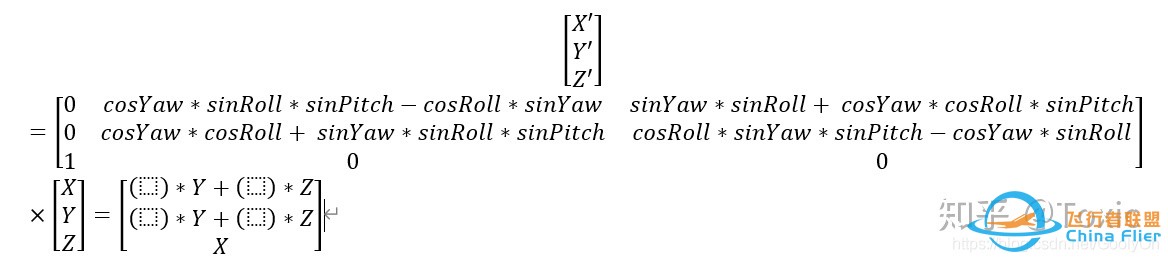
通过这个矩阵我们可以看出,不管Y,Z轴如何旋转X轴都不变。
DCM的实际应用
讲了那么多,是应该用实践上战场了,看看这个DCM究竟有何用!
加速度计计算初始姿态角
一般我们在初始化姿态角的时候,都会用加速度计来初始化飞机的横滚和俯仰角,由于加速度计在Z轴上的转动不会产生变化,所以不能计算偏航角,偏航角需要由磁力计获取! 同样先确定好坐标系,和旋转顺序。我们为什么选用ENU呢?这和传感器有关,我们截取数据手册加速度的方向定义:
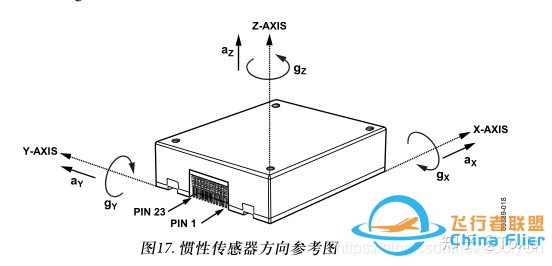
这个IMU的加速度计的坐标系正好符合东北天,所以我们用东北天,如果你系统中使用的是NED,那么这里就要把传感器的Y,Z轴取反,所以第一步确立你的坐标系,以后就统一使用它。
ENU-Z-X-Y

NED-Z-Y-X
注意:由于IMU的坐标系和NED不一致,所以我们要把传感器的Y轴和Z轴的值取反,乘以静止加速度向量的时候,Z轴也要取反,所以是乘以[0,0,-1],这一点很重要!不然,你计算出来的姿态角度是不对的!

磁力计计算初始偏航角
由于加速度计无法感知Z轴变化,所以无法通过加速度计来计算偏航角,还好我们有磁力计,我们可以通过磁力计来计算初始偏航角。参考链接:基于加速度计与磁力计的姿态解算方法(加计补偿偏航)
磁力计原理
地磁场是一个矢量,对于一个固定的地点来说,这个矢量可以被分解为两个与当地水平面平行的分量和一个与当地水平面垂直的分量。如果保持电子罗盘和当地的水平面平行,那么罗盘中磁力计的三个轴就和这三个分量对应起来,如图所示。
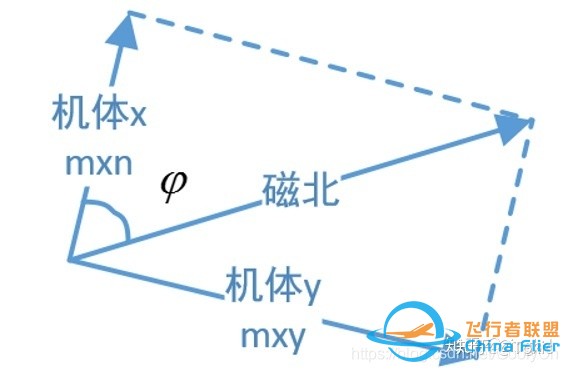
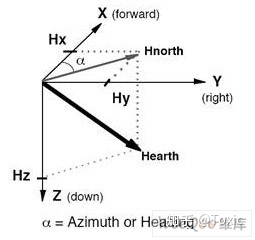
实际上对水平方向的两个分量来说,他们的矢量和总是指向磁北的。罗盘中的航向角(Azimuth)就是当前方向和磁北的夹角。由于罗盘保持水平,只需要用磁力计水平方向两轴(通常为X轴和Y轴)的检测数据就可以用如下公式计算出航向角。当罗盘水平旋转的时候,航向角在0°~ 360°之间变化。
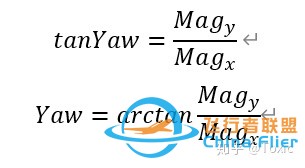
实际航向
实际情况下但是我们不能保证当前载体绝对水平,所以我们需要把传感器的数据转换到水平面。这里就要用到当前飞机的姿态角了,我们通过DCM矩阵来完成从载体系到参考系的转换,我们需要的是参考系下的水平分量。 通过矩阵来表达也就是:
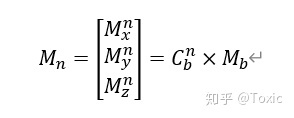
令磁力计测量的数据为:
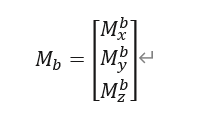
DCM矩阵为(我们使用的是北东地下的ZYX旋转):
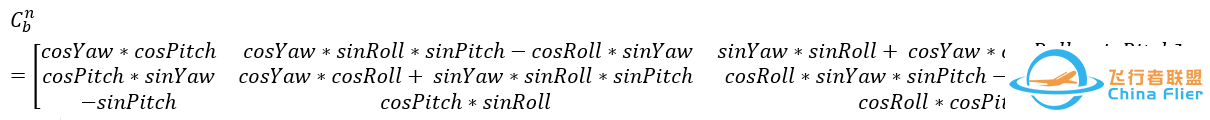
由于Yaw不参与转换,所以设Yaw=0,得到:
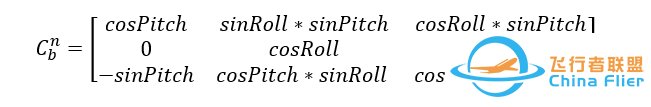
整理公式得到:
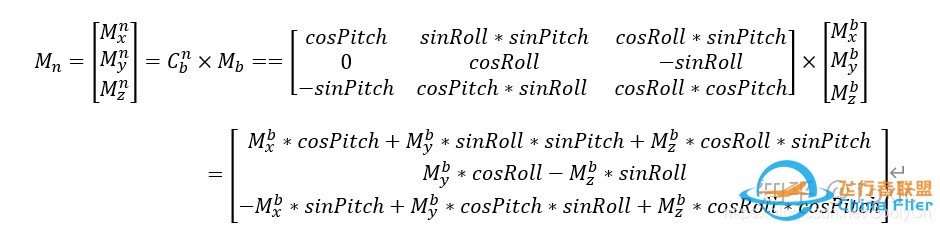
通过这个旋转,我们就把载体坐标系的数据,变成了水平载体坐标系,也就是载体水平的情况下,磁力计测量的数据值。
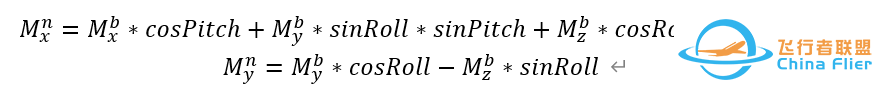
主意z轴的正负(原始数据是z轴朝上为正) 最后得到实际的航向角为:
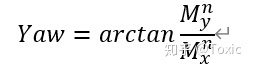
真实航向
磁力计所解算的航向角是载体坐标x轴相对于磁北而言的,而真北与磁北之间存在一个磁偏角:
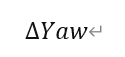
所以载体坐标纵轴相对于真北的航向角为:
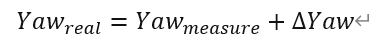
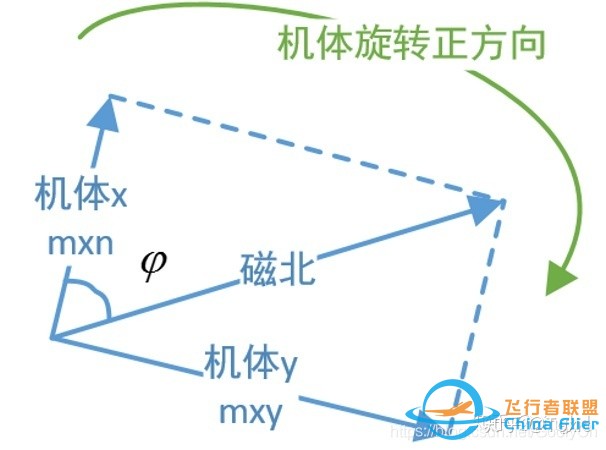
计算出来的夹角是正还是负? 和载体坐标系有关,如果z轴朝下,根据右手定则,那么载体的旋转正方向为顺时针,那么得到的偏航角就是负的。
小结
在实际的系统中使用的时候一定要确定一种旋转方式,不能混用,后面的章节里我们都使用NED参考系下的ZYX内旋。
五、四元数
四元数是一个比较抽象的概念,他是站在四维空间的角度看待三维的旋转变化,比较难以理解。你可以简单的理解为,三维空间中的三轴旋转等价于绕某一个轴进行一个角度的旋转,这是比较好理解的,其实这个和Axis Angle轴角的概念很像了。
四元数如何表达旋转
四元数如何表示姿态?三维空间的任意旋转,都可以用绕三维空间的某个轴旋转过某个角度来表示,即所谓的Axis-Angle表示方法。物体从一个姿态变化到另一个姿态,可等效为物体绕了某一个轴通过一次旋转某个角度完成,但实际物体可能经过了多次中间过程才变化到了我们想要的姿态,我们不去关心中间过程,我们只需找到一种变化关系,通过这种变换关系,可求出物体从地理坐标系变到物体坐标系坐标或者从物体坐标系变到地理坐标系的坐标。
四元数表达式
我们用罗德里格旋转来用四元数表达姿态: 四元数特性:
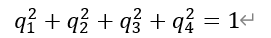
我们这里直接给出四元数下的ZYX旋转矩阵:
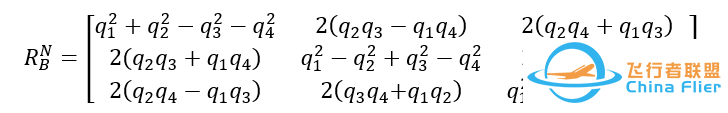
注意:这里四元数旋转矩阵是唯一的。但是为什么注明ZYX旋转呢?那是应为,欧拉角和四元数之间的转换是区分旋转顺序的,不同的旋转顺序会生成不同的四元数,你可以通过四元数在线来观察其中的变化,你可以看出同一种旋转结果,只对应一个四元数,确对应了多种的欧拉旋转顺序。
对四元数矩阵推导感兴趣的朋友参考我这篇文章:
四元数转欧拉角
回顾一下,我们前面得到了欧拉角转DCM,现在我们有了四元数转DCM,把两者的矩阵一对应,就可以求解四元数转欧拉角的方程了。
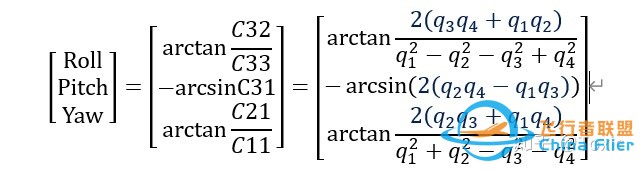
NED_ZYX_Quat2Angle
注意:我们用的NED下的ZYX旋转

根据矩阵对应得到:
ENU_ZXY_Quat2Angle

欧拉角转四元数
Z-Y-X的欧拉角转四元数
我们用的ZYX旋转四元数

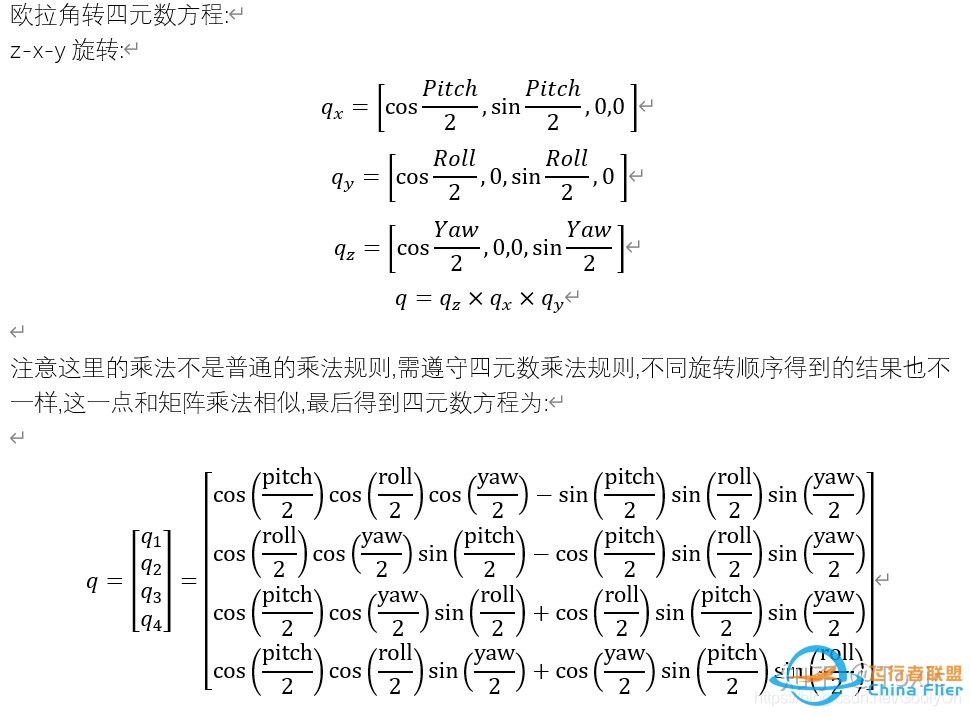
注意:这里的乘法不是普通的乘法规则,需遵守四元数乘法规则,不同旋转顺序得到的结果也不一样,这一点和矩阵乘法相似,最后得到四元数方程为:

Z-X-Y的欧拉角转四元数
ZXY旋转
小结
其实这些方程,我们在Matlab中的Aero Toolbox中,可以找到所有的旋转关系对应。 |
|