|
|
这篇来写一写飞行器的轨迹规划,依然是自娱自乐学习 Coursera 公开课的流水报告。标题图来自 Vijay Kumar 教授的公开课讲义。 轨迹规划问题
无人机飞行器的一个基本技能点,就是要能自己从起点移动到指定的终点,途中还要避开可能的障碍物。例如,在一个大楼内部,如果要让飞行器充当个快递小哥的角色,或者发生火灾、自然灾害时要无人机第一时间飞去有危险隐患的现场进行侦察时,飞行器在迂回的走廊上穿梭、上下楼梯,途中要避开墙壁、找到楼梯的位置,从而抵达目的地完成后续任务。

市面上常见的四轴无人机飞行器
这大约就是所谓的轨迹规划(trajectory planning)问题。我们可以先指定一些时刻,规定飞行器必须经过指定的航点(waypoint)。更进一步,我们希望无人机可以根据航点的信息,自行计算出一条合适的路线,依次通过各个航点,依次最终到达终点。如何根据这些航点,规划出一条光滑性、可控性都足够好的轨迹,就是本篇要讨论的问题。
在我们生活的空间中,飞行器的轨迹规划将会涉及到 x(t),y(t) 和 z(t) 三个维度的运动。为了表述方便,我们把位移函数写成矢量形式
r(t) = \left( \begin{array}{c} x(t) \\ y(t) \\ z(t) \end{array} \right) \\
设包括起点和终点在内的航点共有 n+1 个。在时刻 T_k,飞行器需要到达事前定义好的第 k 个航点 R_k。对应于 k=1 的 R_1 即代表飞行的起点,对应于 k=n+1 的 R_{n+1} 即代表飞行的终点。我们将航点记为
R_k (T_k) = \left( \begin{array}{c} X_k \\ Y_k \\ Z_k \end{array} \right) \qquad k=1,2,\cdots,n,n+1 \\
其中,R_k 的具体位置可以由事先定义好的坐标参数 X_k、Y_k 和 Z_k 给出。
由此,我们需要规划的路线共被分成 n 段。待解决的核心问题,就是该如何确定这 n 个分段函数。
加加速度最小化
不少学者在研究中发现,许多生活中常见的和工程中的实际问题,不仅要考虑我们熟悉的加速度,还要考虑加速度的变化率,即加加速度(jerk,中文也有译作跃度、急动度)。根据牛顿定律,很容易知道,加加速度意味着力在发生变化:
\frac{\mathrm{d} F}{\mathrm{d} t} = \frac{\mathrm{d} (ma)}{\mathrm{d} t} = m \frac{\mathrm{d} a}{\mathrm{d} t} = mj \\
比如车辆启动、急速转向时,不仅有加速度,还会有加加速度,作用在人体上的力也在变化,这种状态可能会让乘客感到难受,因此汽车工程师会用加加速度作为评判乘客舒适程度的指标。
由加加速度引起的效应在不少工程应用中已被广泛注意到。例如在过山车的设计中,太大的加加速度可能导致人体肌肉来不及做出反应,对人体组织造成伤害,所以设计时需要衡量加加速度的影响。在电梯速度设计中,如果加加速度偏大,也会使得乘坐体验不佳。在制造工业中,如果零件运动的加加速度较大,会导致机床刀具提前老化磨损,因此现代运动控制工程中也会引入加加速度这一参数。
在飞行器的轨迹规划问题中,我们也可以把加加速度纳入考量。由于到飞行器的动力输出决定了加速度,但我们希望动力输出的变化要尽可能平缓,动力忽然增大或者陡然减小的急剧变化都不容易控制,所以就要求加速度随时间的变化是连续且可导的光滑函数,如此就对位移的更高阶导数——加加速度,提出了要求。
Vijay Kumar 教授在公开课提出了 minimum jerk trajectory(加加速度最小化)作为最优路径的方案,正是出于上述的考虑。这个出发点很简洁而且很有道理,本文后面就会按这个思路来做计算。我在网上查到的文献中,我发现也有很多研究者通过使加加速度最小化来求解最优路径。这里顺便可以提一个很有意思的点,有研究表明,我们凭着本能将自己的手从某个起始位置移动到某个目标位置时,实际的路径可以使得加加速度非常接近极小值,千百万年的进化过程中我们学会了如何最省力地移动我们的手。
不过 Vijay Kumar 教授的研究团队采取的最终策略是 minimum snap trajectory,即让全程的加加加速度(是的,三个加字,位移函数的四阶导数,原文为 snap,我不知道这东西有没有对应的中文翻译)最小化。之所以教授要取更高阶的导数,是因为他注意到了为了使飞行器每时每刻在各个方向上都能产生合适的加速度,就要求每时每刻要输出一个合适的力矩(torque)进行姿态控制,如果希望力矩的变化同样是平滑没有突变的,就对描述飞行器姿态的几个欧拉角的变化率有了约束,而这就引出了对位移函数的更高阶导数的要求。
相比于 minimum jerk 的方案,minimum snap 的方案会让计算的复杂程度加大不少。但是 minimum jerk 的方案也可以将力矩不要剧烈变化的约束通过边界条件引入进来,因此产生的结果也不差。所以我在自己瞎折腾的时候,决定采取相对容易一些的加加速度最小化的方案。
具体而言,所谓的 minimum jerk,是要使得如下的作用量(action)取得极小值:
S = \int_{\text{initial}}^{\text{final}} L(r,\dot{r},\ddot{r},\dddot{r}) \, \mathrm{d}t = \int_{\text{initial}}^{\text{final}} (\dddot{r})^2 \mathrm{d}t \\
我们要寻找的,就是能够使得 S 取得极小值并且符合边界条件的函数 r(t)。
这类极值问题可以通过变分法(variational principle)来解决。我之前写过一篇关于变分法的文章,这里不再展开,对这部分数学工具不熟悉的读者可以点击这里。
不难将 Euler-Lagrange 方程稍作推广,有
\frac{\partial L}{\partial r} - \frac{\mathrm{d}}{\mathrm{d}t} \frac{\partial L}{\partial \dot{r}} + \frac{\mathrm{d}^2}{\mathrm{d}t^2} \frac{\partial L}{\partial \ddot{r}} - \frac{\mathrm{d}^3}{\mathrm{d}t^3} \frac{\partial L}{\partial \dddot{r}} = 0 \\
将 L=(\dddot{r})^2 代入后,得到加加速度最小化的路径需要满足:
\frac{\mathrm{d}^6 r}{\mathrm{d}t^6} = 0 \\
上式说明,在每两个相邻的航点之间,我们需要寻找的位移函数 x(t)、y(t) 和 z(t) 均可以由一个 5 阶多项式来描述。
若只关注 x 维度上的运动,在第 k 个航点和第 k+1 个航点之间,有
x_k(t) = a_k t^5 + b_k t^4 + c_k t^3 + d_k t^2 + e_k t + f_k \\
每个分段将会出现 6 个待定的系数 a, b, c, d, e, f。需要规划的路线共有 n 段。因此这个路线规划问题将有 6n 个需要解出的参数。算上 y 和 z 两个维度,需要求解的参数总计就有 18n 个。
显然,要解出这么多的未知数,我们需要足够多的约束条件,才可以建立足够多的方程,从而把这些未知参数通通接出来。这并不是一个简单的问题。不过好在现在已经有了明确的方向,接下来我们就来继续讨论该如何建立需要的 18n 个参数方程。
参数求解
好在我们的轨迹规划问题中,三个维度的运动规划可以视作是相互独立的,能解决一维的问题,也就可以照葫芦画瓢解决另外两个维度。
为了讨论的方便,我们先只关注 x 方向上的运动,先来讨论 n 个分段函数 x_k(t) 总计 6n 个多项式系数该如何确定。
首先,在每个分段的开始和结束,对应的多项式函数必须给出和航点吻合的坐标,我们有:
\begin{aligned} x_k(T_k) &= X_k \\ x_k(T_{k+1}) &= X_{k+1} \end{aligned} \qquad k=1,2,\cdots,n \\
或者写成展开后的形式:
\begin{aligned} a_k T_k^5 + b_k T_k^4 + c_k T_k^3 + d_k T_k^2 + e_k T_k + f_k &= X_k \\ a_k T_{k+1}^5 + b_k T_{k+1}^4 + c_k T_{k+1}^3 + d_k T_{k+1}^2 + e_k T_{k+1} + f_k &= X_{k+1} \end{aligned} \qquad k=1,2,\cdots,n \\
小计有 2n 条方程。
在整个飞行的开始和结束,我们约定无人机的初末速度、初末加速度都为零:
\begin{aligned} x_1'(T_1) = x_n'(T_{n+1}) &= 0 \\ x_1''(T_1) = x_n''(T_{n+1}) &= 0 \\ \end{aligned} \\
具体展开有:
\begin{aligned} 5a_1 T_1^4 + 4b_1T_1^3 + 3c_1T_1^2 +2d_1T_1+e_1 &= 0 \\ 5a_n T_{n+1}^4 + 4b_nT_{n+1}^3 + 3c_nT_{n+1}^2 +2d_nT_{n+1}+e_n &= 0 \\ 20a_1 T_1^3 + 12b_1T_1^2 + 6c_1T_1 +2d_1 &= 0 \\ 20a_n T_{n+1}^3 + 12b_nT_{n+1}^2 + 6c_nT_{n+1} +2d_n &= 0 \end{aligned} \\
小计有 4 条方程。
此外,第 k 个分段和第 k+1 个分段的衔接应该是丝滑的,速度、加速度不该有突变:
\begin{aligned} x_k'(T_{k+1}) - x'_{k+1}(T_{k+1}) &=0\\ x_k''(T_{k+1}) - x''_{k+1}(T_{k+1}) &=0\\ \end{aligned} \qquad k=1,2,\cdots,n-1 \\
其写开的形式为:
\begin{aligned} &5a_k T_{k+1}^4 + 4b_kT_{k+1}^3 + 3c_kT_{k+1}^2 +2d_kT_{k+1}+e_k & \\ & \qquad - 5a_{k+1} T_{k+1}^4 - 4b_{k+1}T_{k+1}^3 - 3c_{k+1}T_{k+1}^2 - 2d_{k+1}T_{k+1} - e_{k+1} = 0\\ &20a_k T_{k+1}^3 + 12b_kT_{k+1}^2 + 6c_kT_{k+1} +2d_k &\\ & \qquad - 20a_{k+1} T_{k+1}^3 - 12b_{k+1}T_{k+1}^2 - 6c_{k+1}T_{k+1} - 2d_{k+1} = 0\\ \end{aligned} \\
小计 2(n-1) 条方程。
为了进一步保证力矩输出能够平缓变化,我们对分段边界上的三阶、四阶导数的连续性进行约束:
\begin{aligned} x_k'''(T_{k+1}) - x'''_{k+1}(T_{k+1}) &=0\\ x_k''''(T_{k+1}) - x''''_{k+1}(T_{k+1}) &=0\\ \end{aligned} \qquad k=1,2,\cdots,n-1 \\
其写开的形式为:
\begin{aligned} &60a_k T_{k+1}^2 + 24b_kT_{k+1} + 6c_k &\\ & \qquad - 60a_{k+1} T_{k+1}^2 - 24b_{k+1}T_{k+1} - 6c_{k+1} = 0\\ &120a_k T_{k+1} + 24b_k - 120a_{k+1} T_{k+1} - 24b_{k+1} = 0\\ \end{aligned} \\
小计也是 2(n-1) 条方程。
如此一来,我们可以建立
2n + 4 +2(n-1)+2(n-1)=6n \\
条方程,恰好等于待解的未知系数的个数!
再进一步,将这含有 6n 个方程的方程组写成矩阵的形式,然后通过求系数矩阵的逆(inverse),全部 6n 个系数就可以被搞定了,这样 x 方向上的每个分段函数就都被确定下来,这个维度的轨迹规划就完成了。
类似地搞定 y(t) 和 z(t) 两个维度的位移函数,如此整个三维的轨迹规划问题也大功告成!
数值模拟
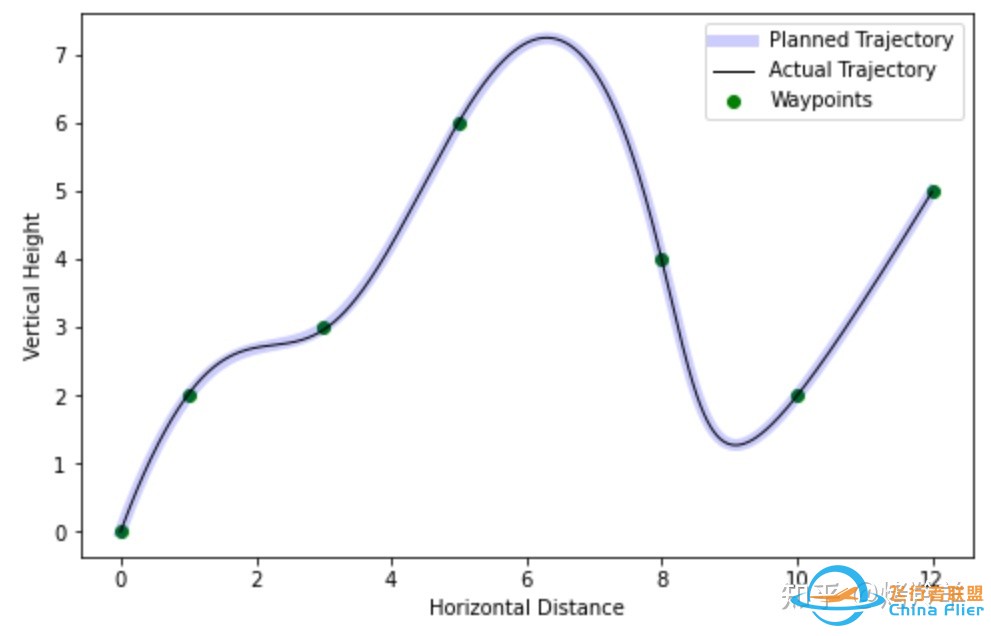
实际模拟中,我还没有尝试去写三维运动的模拟程序,就只做了二维运动的轨迹规划和测试。
我将运动限制在 y-z 平面内,设定了一些航点,然后建立好待解方程组的系数矩阵后,最后调用 Python + numpy 下面的线性代数模块,计算出了所有分段函数的多项式系数。

可以看到,计算出来的轨迹还是一条挺有意思的曲线。它远远称不上连接航点的最短路线。经过每个航点后由着惯性冲过头那么一丢丢,然后慢慢地转向下一个航点。这个行为正保证了飞行过程的平稳。
我将计算出的轨迹输入给上次就写好的的 PD 控制器。文章传送门在这里:
顺手测试了下飞行器在模拟环境中是否能在这条 minimum jerk trajectory 上有出色的表现,结果出奇得棒。
模拟和测试的代码继续给我的 GitHub 屎山仓库添砖加瓦。
好了,这期的灌水文章就到这里了。往后希望自己能把三维的模拟器也写出来,这门有关无人机控制的公开课也算给自己一个很好的交代了。
补充说明和参考文献
人类将手从一个位置移动到另一个位置会遵循加加速度最小化的轨迹,可参考:
T. Flash, N. Hogan, The coordination of arm movements: an experimentally confirmed mathematical model, Journal of Neuroscience, Vol. 5(7), pp. 1688-1703, 1985 利用 minimum jerk 来计算无人机飞行器轨迹的文章有不少,这是其中一篇:
A. Piazzi, A. Visioli, Global minimum-jerk trajectory planning of robot manipulators, IEEE Trans. Ind. Electron., Vol. 47, Issue 1, pp. 140-149, 2000 Vijay Kumar 教授团队的 minimum snap trajectory planning 的高引论文:
D. Mellinger and V. Kumar, "Minimum snap trajectory generation and control for quadrotors," 2011 IEEE International Conference on Robotics and Automation, pp. 2520-2525, 2011 以及 Vijay Kumar 教授团队的课题网页,里面有很多他们在做的有关飞行器控制的其他研究方向。
也有学者利用 minimum variance 来确定最优轨迹的做法,可参考:
Ch. Harris and D. Wolpert, Signal-dependent noise determines motor planning, Nature, Vol. 394, pp. 780-784, August 1998 以及目标 minimum torque change 来计算最优轨迹的做法:
Y. Uno, M. Kawato, R. Suzuki, Formation and control of optimal trajectory in human multijoint arm movement, Biological Cybernetics, Vol. 61, pp. 89-101, 1989
E. Nakano, H. Imamizu, R. Osu, Y. Uno, H. Gomi, T. Yoshioka, M. Kawato, Quantitative examinations of internal representations for arm trajectory planning: minimum commanded torque change model, Journal of Neurophysiology, Vol. 81, pp.2140-2155, 1999 对于如何定义最优轨迹,即如何选择合适的目标函数,这有一篇挺棒的综述文章:
E. Todorov, Optimality principles in sensorimotor control, Nature Neuroscience, Vol.7 (9), pp.907-915, Sept 2004 最后,理论物理狗还是要表示并不是那么喜欢 minimum jerk trajectory 这套算法。经典力学里有一个 Ostrogradsky 定理,说的大约是只要 Lagrangian 里边涉及到了坐标的二阶以上的高阶导数,可以写出的 Hamiltonian 虽然可以表现得像是能量那样有守恒的性质,但是这个 Hamiltonian 的稳定性会一塌糊涂,甚至连极小值都不存在。但搞工程的大概完全不会 care 这些事情吧。。。 |
|