自动驾驶路径规划-Graph Based的BFS最短路径规划

han1314

自动驾驶运动规划(Motion Planning)中提到Mission Planner关注High-Level的地图级别的规划，通过Graph Based的图搜索算法实现自动驾驶路径的规划。今天看看如何用Python实现Graph Based的BFS最短路径规划。


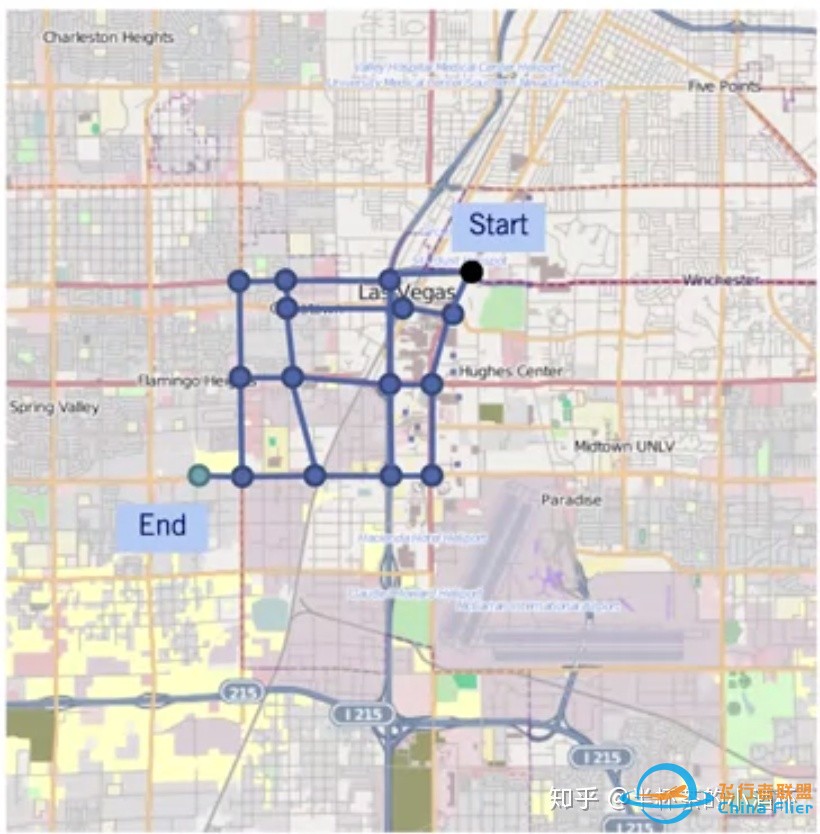
1、Graph的基础定义及Python表达

在数学或者计算机数据结构的教材中，Graph由Node(或者vertices)组成，Node之间以Edge连接(如下图所示)。如果Node之间的连接是没有方向的，则称该Graph为无向图(Undirected Graph)；反之，如果Node之间的连接是有方向的，则称为该Graph为有向图(Directed Graph)；有向图(Directed Graph)的Edge被成为Arc。


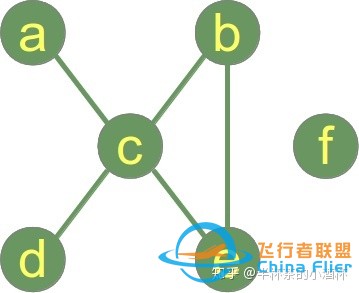
上图的Graph在Python中可以借助Dictionary表达:
graph = { "a" : ["c"],
          "b" : ["c", "e"],
          "c" : ["a", "b", "d", "e"],
          "d" : ["c"],
          "e" : ["c", "b"],
          "f" : []
        }Graph的Edge可以用tuple表达，比如连接a和b的Edge可以表示为(a, b)。我们可以实现一个从Graph生成Edge的函数。
def generate_edges(graph):
    edges = []
    for node in graph:
        for neighbour in graph[node]:
            edges.append((node, neighbour))

    return edges

print(generate_edges(graph))generate_edges()函数生成Graph的所有Edge:
[('a', 'c'), ('c', 'a'), ('c', 'b'), ('c', 'd'), ('c', 'e'), ('b', 'c'), ('b', 'e'), ('e', 'c'), ('e', 'b'), ('d', 'c')]可以看到，由于Node f是孤立节点，所有所有Edge中都不包含Node f。
2、Python实现基础Graph类

在了解Graph的基础概念之后，用Python实现一个Graph类。
""" A Python Class
A simple Python graph class, demonstrating the essential
facts and functionalities of graphs.
"""

class Graph(object):
    def __init__(self, graph_dict=None):
        """ initializes a graph object
            If no dictionary or None is given,
            an empty dictionary will be used
        """
        if graph_dict == None:
            graph_dict = {}
        self.__graph_dict = graph_dict

    def vertices(self):
        """ returns the vertices of a graph """
        return list(self.__graph_dict.keys())

    def edges(self):
        """ returns the edges of a graph """
        return self.__generate_edges()

    def add_vertex(self, vertex):
        """ If the vertex "vertex" is not in
            self.__graph_dict, a key "vertex" with an empty
            list as a value is added to the dictionary.
            Otherwise nothing has to be done.
        """
        if vertex not in self.__graph_dict:
            self.__graph_dict[vertex] = []

    def add_edge(self, edge):
        """ assumes that edge is of type set, tuple or list;
            between two vertices can be multiple edges!
        """
        edge = set(edge)
        (vertex1, vertex2) = tuple(edge)
        if vertex1 in self.__graph_dict:
            self.__graph_dict[vertex1].append(vertex2)
        else:
            self.__graph_dict[vertex1] = [vertex2]

    def __generate_edges(self):
        """ A static method generating the edges of the
            graph "graph". Edges are represented as sets
            with one (a loop back to the vertex) or two
            vertices
        """
        edges = []
        for vertex in self.__graph_dict:
            for neighbour in self.__graph_dict[vertex]:
                if {neighbour, vertex} not in edges:
                    edges.append({vertex, neighbour})
        return edges

    def __str__(self):
        res = "vertices: "
        for k in self.__graph_dict:
            res += str(k) + " "
        res += "\nedges: "
        for edge in self.__generate_edges():
            res += str(edge) + " "
        return res测试一下Graph类的实现。


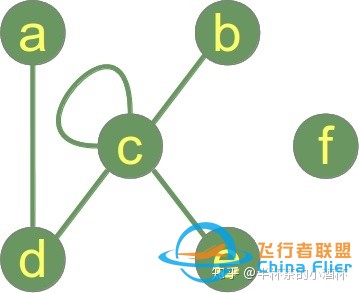
if __name__ == "__main__":
    g = { "a" : ["d"],
          "b" : ["c"],
          "c" : ["b", "c", "d", "e"],
          "d" : ["a", "c"],
          "e" : ["c"],
          "f" : []
        }


    graph = Graph(g)

    print("Vertices of graph:")
    print(graph.vertices())

    print("Edges of graph:")
    print(graph.edges())

    print("Add vertex:")
    graph.add_vertex("z")

    print("Vertices of graph:")
    print(graph.vertices())

    print("Add an edge:")
    graph.add_edge({"a","z"})
   
    print("Vertices of graph:")
    print(graph.vertices())

    print("Edges of graph:")
    print(graph.edges())

    print('Adding an edge {"x","y"} with new vertices:')
    graph.add_edge({"x","y"})
    print("Vertices of graph:")
    print(graph.vertices())
    print("Edges of graph:")
    print(graph.edges())程序的输出如下:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f']
Edges of graph:
[{'a', 'd'}, {'c', 'b'}, {'c'}, {'c', 'd'}, {'c', 'e'}]
Add vertex:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f', 'z']
Add an edge:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f', 'z']
Edges of graph:
[{'a', 'd'}, {'c', 'b'}, {'c'}, {'c', 'd'}, {'c', 'e'}, {'a', 'z'}]
Adding an edge {"x","y"} with new vertices:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f', 'y', 'z']
Edges of graph:
[{'a', 'd'}, {'c', 'b'}, {'c'}, {'c', 'd'}, {'c', 'e'}, {'a', 'z'}, {'y', 'x'}]3、Graph中的路径查找(Path Finding)

有了Graph结构之后，我们看看如何实现查找从一个Node到另一个Node的路径的问题。在实现Python代码之前，我们再复习一些概念：
邻接节点(Adjacent Vertices)：如果两个Vertices存在一条连接Edge，则称它们是相邻接的。
无向图中的Path: 无向图中的Path是一个点序列P = (v_1, v_2, ..., v_n)，序列中相邻的节点都是相邻接的。
简单路径(Simple Path)：没有重复节点的Path称为Simple Path。
3.1 Graph中路径查找的递归实现

实现查找一条从开始顶点(Start Vertex)到结束顶点(End Vertex)的简单路径(Simple Path) 的算法。
def find_path(self, start_vertex, end_vertex, path=None):
    """ find a path from start_vertex to end_vertex
        in graph """
    if path == None:
        path = []
    graph = self.__graph_dict
    path = path + [start_vertex]
    if start_vertex == end_vertex:
        return path
    if start_vertex not in graph:
         return None
    for vertex in graph[start_vertex]:
        if vertex not in path:
            extended_path = self.find_path(vertex,
                                           end_vertex,
                                           path)
            if extended_path:
                return extended_path
    return None查找从开始顶点(Start Vertex)到结束顶点(End Vertex)的所有简单路径(Simple Path)的算法。
def find_all_paths(self, start_vertex, end_vertex, path=[]):
    """ find all paths from start_vertex to
        end_vertex in graph """
    graph = self.__graph_dict
    path = path + [start_vertex]
    if start_vertex == end_vertex:
        return [path]
    if start_vertex not in graph:
        return []
    paths = []
    for vertex in graph[start_vertex]:
        if vertex not in path:
            extended_paths = self.find_all_paths(vertex,
                                                 end_vertex,
                                                 path)
            for p in extended_paths:
                paths.append(p)
    return paths查找从开始顶点(Start Vertex)到结束顶点(End Vertex)的最短路径(Simple Path)的算法。
def findShortestPath(graph,start,end,path=[]):
    path = path +[start]
    if start == end:
        return path
   
    shortestPath = []
    for node in graph[start]:
        if node not in path:
            newpath = findShortestPath(graph,node,end,path)
            if newpath:
                if not shortestPath or len(newpath)<len(shortestPath):
                    shortestPath = newpath测试代码如下:
g = { "a" : ["d"],
      "b" : ["c"],
      "c" : ["b", "c", "d", "e"],
      "d" : ["a", "c"],
      "e" : ["c"],
      "f" : []
    }

graph = Graph(g)

print('The path from vertex "a" to vertex "b":')
path = graph.find_path("a", "b")
print(path)

print('All paths from vertex "a" to vertex "b":')
path = graph.find_all_paths("a", "b")
print(path)路径查找的结果如下:
The path from vertex "a" to vertex "b": ['a', 'd', 'c', 'b']

All paths from vertex "a" to vertex "b":
[['a', 'd', 'c', 'b'], ['a', 'f', 'd', 'c', 'b']]3.2 Graph路径查找的非递归实现

Graph中查询最短路径的非递归遍历算法利用Queue的先进先出的特性，以起点Node为中心，波浪式的向外查找，直至找到目标Node。这种波浪式的查找方法，保证了找到的一定是起点Node到终点Node的最短路径。在查找过程中，记录了查询路径上所有Node的前驱节点，从而保证了在查到目标节点之后能够追溯到完整的路径。


Python的实现代码如下：
def extractPath(self, u, pred):
    path = []
    k = u
    path.append(k)
    while k in pred:
        path.append(pred[k])
        k = pred[k]
        
    path.reverse()
   
    return path
   
def findShortestPath(self, start, end, path=[]):
    # Mark all the vertices as not visited
    closed = set()
     
    # Create a queue for BFS
    opened = []
    pred = {}
  
    # Mark the source node as visited and enqueue it
    opened.append(start)
    closed.add(start)
  
    while opened:
        u = opened.pop(0)
        if u == end:
            path = self.extractPath(u, pred)
            return path
  
        for i in self.__graph_dict:
            if i not in closed:
                opened.append(i)
                pred = u
                closed.add(i)测试代码如下：
g = { "a" : ["d"],
      "b" : ["c"],
      "c" : ["b", "c", "d", "e"],
      "d" : ["a", "c"],
      "e" : ["c"],
      "f" : []
    }

graph = Graph(g)

print('The path from vertex "a" to vertex "b":')
path = graph.findShortestPath("a", "b")
print(path)输出最短路径：
The path from vertex "a" to vertex "b":
['a', 'd', 'c', 'b']4、Mission Planner的路径规划

目前为止，我们已经知道，在路径规划技术中，首先将地图构建为Node-Edge的Graph结构，然后基于Graph和BFS算法实现从起始Node和目的地Node的路径查找。但是，我们必须知道到，本文介绍的路径规划是Graph的所有Edge权重是完全相等，这是不符合实际情况的，实际的工程应用的路径规划要更为复杂，要考虑到道路交通状况、路径长度、到达时间、乘客上下车位置等等，每个Edge都会赋予不同的权重，不同的权重表达了该Edge被选中的可能性。后面我们将继续学习在有权重的Graph中如何实现路径查找。
参考链接

1、Graphs in Python
2、Coursera多伦多大学自动驾驶课程-Motion Planning for Self-Driving Cars

注：本文首发于微信公众号，转载请注明出处，谢谢！



公众号:半杯茶的小酒杯

个人博客地址:
推荐阅读：