[飞控]倾转分离(一)-APM的倾转分离竟然没有效果？

frag86@126.com

通过之前的文章
我们看到APM的源码虽然做了轴角分离，但是对yaw的限制处理不够，但是这样的处理到底有什么效果呢？我把这段程序用MATLAB移植了，可以直观的从数字上看到结果。
思路：设置相同的当前姿态，和期望姿态，分别用直接四元数计算误差，和倾转分离后四元数计算误差，然后分别转成轴角，这个轴角就是控制器接收到的误差，我们来看看这个两组数据上有什么区别。（最后有一段程序是单独现在z轴的，但是默认是26度，而且需要姿态更新到下一周期生效，这一部分先不考虑，所以这次对比保持z轴在26度以内）
实验：
为了直观，设置姿态使用欧拉角形式 单位 度
当前姿态【0,0,0】，期望姿态【30,30,25】
误差为轴角形式  单位 度
直接计算误差为【22.3280 ，35.0479 ，16.0488】   简称【完全误差】
倾转分离误差为【16.9144 ，37.8010 ，16.7880】   简称【分离误差】
从数字上来看，z轴的误差区别不大，主要是x,y轴的误差有区别，但也相差不多。
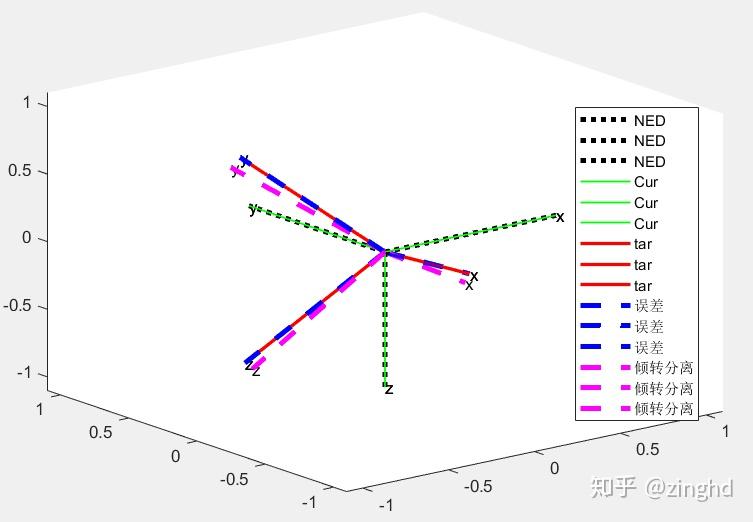
为了直观我们把对应的姿态画出来，
绿色为当前姿态，和黑色的NED坐标系是重合的，
红色为期望姿态，和蓝色的【完全误差】是重合的，很好理解，因为完全误差就是全部的误差，所以当前姿态加上全部的姿态肯定和期望姿态完全重合。
粉红色的是【分离误差】，因为是处理后的误差所以，无法和期望误差完全重合，但是，z轴也没有对齐，这点有些出乎意料，原本我以为倾转分离的目标就是z轴对齐，然后x,y有点误差。


于是我把中间过程也分析了一下。
先计算中间过程 也就是对齐z轴的过程，简称【倾斜误差】
【倾斜误差】为【19.8108 ，37.1418 ，6.7148】


可以看到，【倾斜误差】确实可以把z轴对齐，这个和我们想的是一样的。
然后计算【旋转误差】= 【0.0000 ，0.0000 ，16.7880】，
把这【倾斜误差】和【旋转误差】组合，蓝色的坐标系 完全重合与 红色的期望姿态。（这里的组合是先旋转后倾斜，因为我们计算的时候是先倾斜后旋转）


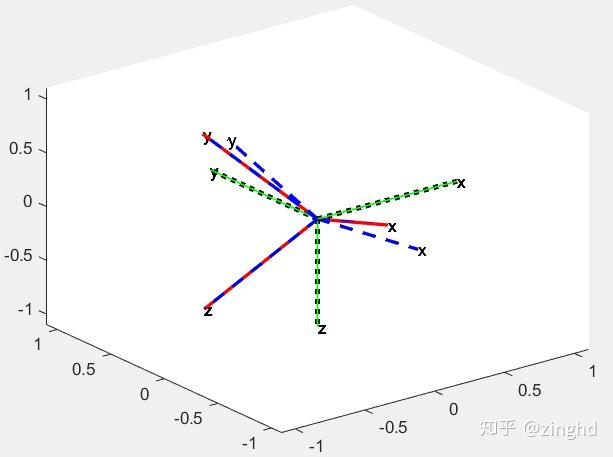
也就是说，分离出来的两次旋转没有错误，【倾斜误差】可以对其z轴，【旋转误差】可以对其偏航。
但是因为APM  直接把【倾斜误差】的z轴数据给抛弃了，所以导致，最后的误差连z轴都对不齐。
Vector3f rotation;
    thrust_vec_correction_quat.to_axis_angle(rotation);
    att_diff_angle.x = rotation.x;
    att_diff_angle.y = rotation.y;
yaw_vec_correction_quat.to_axis_angle(rotation);
    att_diff_angle.z = rotation.z;
这个现象确实和想象中我不一样，
我看 APM 程序的时候最大的两个疑惑
1.为什么倾转分离后没对 yaw 做处理（26度以内的yaw）
2.为什么直接抛弃【倾斜误差】的z轴，难道是为了限制yaw？
现在看来，这两个疑惑都和实验吻合了，因为没对yaw做限制，所以【完全误差】和【分离误差】的 yaw 几乎一致，因为抛弃了【倾斜误差】的z轴，所以最后连z轴都对不齐。
为了解决这个疑惑我又去看了 PX4 的算法，没想到 PX4 的算法更新了，初步看了一下，又多了个几个疑惑
3.为什么 APM 说是四元数算法，但是过程中各种转旋转矩阵，转轴角，转换次数多了会引入新的误差，倒是PX4，一套四元数用到最后才转轴角，并且每次都会归一化来减少误差。
具体细节等下次我来对比 PX4 的算法仔细分析一下。
总结：APM 的算法除了最后的轴角处理感觉很奇怪，之前的过程思路还很清晰很好理解的，主要问题就是就是没有对 yaw 做处理 , 以及抛弃的【倾斜误差】的z轴 ,所以导致实验结果就是，这套算法有倾转分离，和没倾转分离差别不大。
部分源码：
%NED坐标系 当前机体坐标系 期望机体坐标系 （度）
NED=[0 0 0];
Cur_angle=[0 0 0];   
Des_angle=[30 30 25];
%机体坐标系转换为弧度
cur_angle_radian=[Cur_angle(1)*pi/180,Cur_angle(2)*pi/180,Cur_angle(3)*pi/180] ;  
des_angle_radian=[Des_angle(1)*pi/180,Des_angle(2)*pi/180,Des_angle(3)*pi/180];
%在NED下 画出 机体坐标系
plot_rotate_NED([0,0,0],Cur_angle,['g','g','g'],'-',1)
plot_rotate_NED([0,0,0],Des_angle,['r','r','r'],'-',1)

%当前姿态 Ccur->N
cur_dcm= euler2dcm(cur_angle_radian(1),cur_angle_radian(2),cur_angle_radian(3));
att_from_quat=euler2qual( cur_angle_radian(1),cur_angle_radian(2),cur_angle_radian(3) );
%当前姿态的旋转矩阵 取出z轴列（z轴单位向量） Zcur(N)
cur_att_thrust_vec=cur_dcm*[0;0;1];
%期望姿态 Ctar->N
des_dcm = euler2dcm( des_angle_radian(1),des_angle_radian(2),des_angle_radian(3) );
att_to_quat=euler2qual( des_angle_radian(1),des_angle_radian(2),des_angle_radian(3) );
%期望姿态的旋转矩阵 取出z轴列（z轴单位向量） Ztar(N)
des_att_thrust_vec=des_dcm*[0;0;1];

%不使用倾转分离的思路，直接计算 目标姿态-初始姿态=总误差姿态
all_correction_quat = Q_multipli( Q_INV(att_from_quat),att_to_quat );

%%N系下 两个向量的**旋转误差**
thrust_vec_cross=cross(cur_att_thrust_vec,des_att_thrust_vec);
%z轴误差角度 弧度
thrust_vec_dot=acos(dot(cur_att_thrust_vec,des_att_thrust_vec));
thrust_vector_length=norm(thrust_vec_cross);
if( (thrust_vector_length==0) || (thrust_vec_dot==0))
    thrust_vec_cross = [0,0,1];
    thrust_vec_dot = 0.0;
else
    thrust_vec_cross = thrust_vec_cross/thrust_vector_length;
end

%轴角 转 四元数 描述的是 目标转到初始的旋转 所以对应的旋转是 Qtb1->cb 转轴在N系
thrust_vec_correction_quat=axis_angle2Q(thrust_vec_cross,thrust_vec_dot)

%%旋转 Qtb1->cb 转到初始坐标系
thrust_vec_correction_quat=Q_multipli(Q_INV(att_from_quat),Q_multipli(thrust_vec_correction_quat,att_from_quat))

%%画出 初始姿态 加上**倾斜误差** 之后的姿态 结果是 z轴对齐了
plot_rotate_body([0,0,0],Cur_angle,quat2euler(thrust_vec_correction_quat)*57.3,['g','g','g'],'-.',2)
%%画出 初始姿态 加上总误差 之后的姿态 结果是 两个坐标系完全重合
plot_rotate_body([0,0,0],Cur_angle,quat2euler(all_correction_quat)*57.3,['b','b','b'],'--',2)

%Qcb->tb1 * Qn->cb * Qtb->n = Qtb->tb1 (即**旋转误差**)
yaw_vec_correction_quat = Q_multipli(Q_INV(thrust_vec_correction_quat),Q_multipli(Q_INV(att_from_quat),att_to_quat));

all_axis_angle=Q2axis_angle(all_correction_quat);
tilt_axis_angle=Q2axis_angle(thrust_vec_correction_quat);
torsion_axis_angle=Q2axis_angle(yaw_vec_correction_quat);
tilt_torsion_angle=[tilt_axis_angle(1),tilt_axis_angle(2),torsion_axis_angle(3)]*57.3

att_diff_angle_x = tilt_axis_angle(1);
att_diff_angle_y = tilt_axis_angle(2);
att_diff_angle_z = torsion_axis_angle(3);

%att_diff_angle_z 弧度   (0.46弧度 = 26度)
if(att_diff_angle_z > 0.46)      
     att_diff_angle_z = constrain_float(wrap_PI(att_diff_angle_z), -0.46, 0.46);
     yaw_vec_correction_quat=Q_from_axis_angle([0,0,att_diff_angle_z]);
     att_to_quat = Q_multipli( att_from_quat,Q_multipli(thrust_vec_correction_quat,yaw_vec_correction_quat));
end
这个结果很出人意料，所以非常希望各位感兴趣的朋友，加我的微信，多和我交流，如有问题欢迎指正。
关注微信公众号【无人机干货铺】，回复【倾转分离】可以获得这次实验的源码，期待你的关注。

yiying

APM把倾斜误差的轴角和旋转误差的轴角直接相加，个人认为这不合理；同时有点疑问，你上面计算的【倾斜误差】为【19.8108 ，37.1418 ，6.7148】，这里倾斜轴角z分量为什么不是0？

风履

算出来就是这个 你可以验算一遍