|
|
引言
对实际的控制系统而言,采集到的原始信号往往是有噪声的,而噪声往往会对系统的稳定性能产生隐患;或为了提取有用的控制信号,滤除不必要的频域成分,数字滤波技术必不可少,其中最常用的便是一阶低通滤波(LPF)算法。
一阶低通滤波器(Low Pass Filter,LPF),顾名思义就是当输入信号的频率在LPF设定的频率(截止频率)以内时,该信号可以通过(无衰减),而当该信号的频率高于该频率时,则会产生衰减。也就是说,LPF算法可滤除(filter-out)不需要的高频信号,从而保证系统有效的频率成分。
为使大家通过该篇能对LPF以及信号处理技术的应用有一个更为深刻的理解,我将从如下5个方面来说明。
————————————————————————
- 一阶低通滤波器的定义;
- 一阶低通滤波器的数字实现;
- 仿真实例分析;
- 应用实例分析—以APM和PX4飞控两个实例来说明;
- 具体应用中应考虑的问题
————————————————————————
一、一阶低通滤波器的定义
A Low Pass Filter is a circuit that can be designed to modify, reshape or reject all unwanted high frequencies of an electrical signal and accept or pass only those signals wanted by the circuits designer.
对于一阶低通滤波而言,从控制模型上分析就是一个一阶惯性环节,其描述形式如式所示。
H(s) = \frac{1}{\frac{s}{w_c}+1} , w_c = 2\pi*f_c ,其中 f_c 为LPF的截止频率。 (1)
Figure 1给出了一阶低通滤波器在截止频率 f_c = 20Hz ,即 H(s) = \frac{1}{\frac{s}{2\pi*20}+1} 的Bode图。由该图可知,当信号的输入频率 f>(f_c = 20Hz) 时,其信号的幅值 Mag<0dB ,即表示信号将会出现衰减,以此达到滤波的目的。
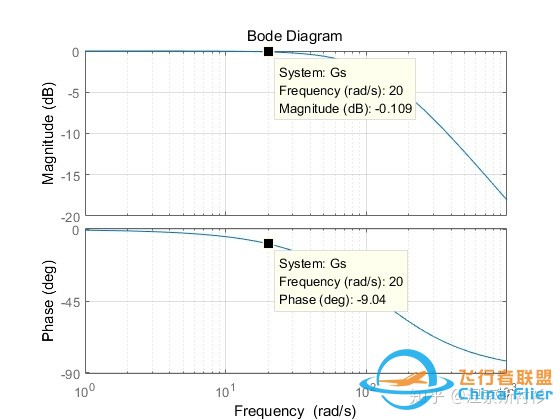
Fig.1 一阶低通滤波Bode图
二、一阶低通滤波器的数字实现
学过电路的都知道,RC电路便可组成一个一阶低通滤波电路(如Figure 2所示)。
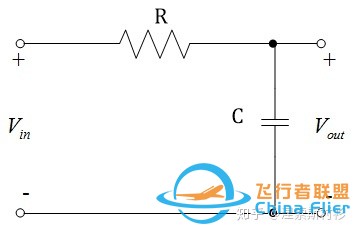
Figure.2 一阶低通滤波原理图
由电路原理的基本知识可知该一阶RC低通滤波电路的输入输出关系(传递函数)为:
H(jw) = \frac{V_{out}}{V_{in}} = \frac{\frac{1}{jwc}}{R+\frac{1}{jwc}} = \frac{1}{jwRC + 1}---(2)
令 s=jw ,则一阶RC低通滤波在S域的传递函数如式(3)所示。将其与式(1)对比可知,有 RC = \frac{1}{2\pi*f_c} ,即可知LPF的截止频率 f_c = \frac{1}{2\pi*RC} 。当我们知道信号的有用频率段,即截止频率f_c 已知时,可设计RC的值。
H(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{RCs+1} , s = jw (3)
为设计数字化滤波器,我们还需对上述连续系统进行离散化处理(z变换)。由以前的知识可知,z变换有许多不同的形式,对于LPF而言,主要采用一阶后向差分法,其数学表达式如式(4)所示:
s = \frac{1-z^{-1}}{T_s} , 其中 T_s 表示采样周期。 (4)
结合式(3)(4),可知LPF的数字化表达式为:
H(z) = \frac{V_{out}(z)}{V_{in}(z)}= \frac{1}{RC\frac{1-z^{-1}}{T_s}+1} = \frac{T_s}{RC(1-z^{-1})+T_s} (5)
变换后可知:
V_{in}(z) = (1+\frac{RC}{T_s})V_{out}(z) - \frac{RC}{T}V_{out}(z)z^{-1} (6)
继续转化差分方程,则有:
V_{in}(n) = (1+\frac{RC}{T_s})V_{out}(n) - \frac{RC}{T_s}V_{out}(n-1) (7)
最终我们可知其LPF的差分表达式如下所示:
V_{out}(n) = V_{out}(n-1) + \frac{T_s}{T_s + RC}(V_{in}(n) - V_{out}(n-1)) (8)
令滤波系数 \alpha = \frac{T_s}{T_s + RC} ,且 \alpha\in[0,1] ,则LPF的差分表达式可改写为:
V_{out}(n) = V_{out}(n-1) + \alpha(V_{in}-V_{out}(n-1)) (9)
对式(9)进行重写,最后可知一阶低通滤波模型为:
V_{out}(n) = (1-\alpha)V_{out}(n-1) + \alpha*V_{in} (10)
对此,LPF完整的数学分析已经完成。在实际应用中,已知采样周期,根据实际的系统设计合适的截止频率 f_c ,即对采集的信号 V_{in}(n) 进行滤波。
三、仿真实例分析
虽然通过前面的分析,知道了LPF数学模型的由来,但实际应用中如何滤波,怎么应用可能不够直观。为使大家有一个更为深刻的理解,特以一个实例来说明。
设一个信号的时域表达式如下所示,即有三个频率成分: f_1=2Hz , f_2=30Hz , f_3=40Hz 叠加而成,其幅值分别为 A_1 = 2, A_2 = 5 , A_3 =1 0 ,令采样周期为 T_s = 0.01s 。
y(t)=2*sin(2\pi*2*t)+5*sin(2\pi*30*t)+10*sin(2\pi*40*t)
为此,设计一截止频率 f_c=10Hz 的低通滤波器,由前面的分析可知,该低通滤波器的滤波为:
\alpha=\frac{T_s}{T_s+RC}=\frac{T_s}{T_s+1/(2*\pi*f_c)}=0.3859
令滤波后的输出为 yc(t) ,由式(10)即可求得滤波后的输出 yc(t) 。图3为滤波前后时域输出图,从该图虽然能直观看出信号有所衰减,但不够直观,而通过对比滤波前后频域输出图(Fig 4)可知,能非常直观地看出频率 f_1=2Hz 的信号幅值没有变化,而频率为 f_2=30Hz , f_3=40Hz 的信号出现了衰减,即当信号的频率大于 所设定的截止频率f_c=10Hz 时,信号便会出现衰减。
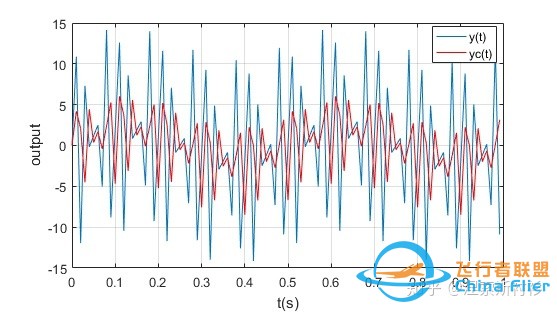
Fig.3 滤波前后时域输出对比
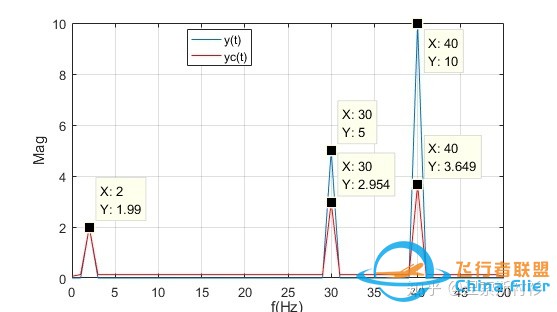
Fig.4 滤波前后频域输出对比
四、应用实例分析
LPF的应用场合很多,相信通过前面的分析,对于其原理与应用应该有了进一步的了解。下面给出无人机飞控中的代码实例,以便能对其他项目的应用有所参考与借鉴。通过第二部分的分析,相信不难理解其中的实现原理及过程。
4.1 APM飞控LPF实例分析
APM开源飞控代码中一阶低通数字滤波器的实现如下所示,详细代码参见LowPassFilter.cpp文件。相信根据上述的分析,不难理解该功能的具体实现。
@input:sample(当前的采样值)V_in(n) cutoff_freq(截止频率) dt(采样周期)
@output:_output(V_out(n))
template <class T>
T DigitalLPF<T>::apply(const T &sample, float cutoff_freq, float dt) {
if (cutoff_freq <= 0.0f || dt <= 0.0f) {
_output = sample;
return _output;
}
float rc = 1.0f/(M_2PI*cutoff_freq);
alpha = constrain_float(dt/(dt+rc), 0.0f, 1.0f);
_output += (sample - _output) * alpha;
return _output;
}
4.2PX4飞控LPF实例分析
PX4开源飞控中LPF的具体实现文件为:.\Firmware\src\lib\controllib\BlockLowPass.cpp,给出实现代码,以便参考。
float BlockLowPass::update(float input)
{
if (!PX4_ISFINITE(getState())) {
setState(input);
}
float b = 2 * float(M_PI) * getFCut() * getDt();
float a = b / (1 + b);
setState(a * input + (1 - a)*getState());
return getState();
}五、具体应用中应考虑的问题
(1)相位滞后问题:一阶低通滤波器虽然能有效滤掉高频成分,但它会产生一定的滞后效应。如Figure 1所示,虽然在截止频率 f_c = 20Hz 处,其幅值为0dB,但相位大致为 -9^{o} ,也就是相较于原来的系统,该频段的输入信号皆产生了延时。
(2)截止频率的选择:对实际的控制系统而言,以APM为例,将滤波器的截止频率一般等于系统的带宽。而系统的带宽怎么确定呢,最粗暴的办法就是根据实际的经验有 fc =f_s/ (4\sim10) ,其中 f_s 为信号的采样频率,这一部分可参见其飞控代码中LPF的接口调用。
六、仿真实例中的代码
Ts = 0.01;
Fs = 1/Ts;
t = [0:0.01:0.99];
f1 = 2;
f2 = 30;
f3 = 40;
y1 = 2*sin(2*pi*f1*t);
y2 = 5*sin(2*pi*f2*t);
y3 = 10*sin(2*pi*f3*t);
y = y1+y2+y3;
fc = 10;
b = 2*pi*fc*Ts;
a = b/(1+b)
a1 = Ts/(Ts+1/(2*pi*fc))
L =length(t);
yc = zeros(L);
yc(1)=y(1);
for j = 2:L
yc(j) = a*y(j)+(1-a)*y(j-1);
end
f = Fs*(0:(L/2))/L;
Y = fft(y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
YC = fft(yc);
P4 = abs(YC/L);
P3 = P4(1:L/2+1);
P3(2:end-1) = 2*P3(2:end-1);
figure(1)
plot(t,y,t,yc);
figure(2)
plot(f,P1,f,P3);<hr/> |
一阶, APM, LPF, PX4, 低通, APM, APM, APM, APM, APM, APM, APM, APM, APM
|